1. 背景 1990 年,William Pugh 提出了一种用于替换平衡树的数据结构 Skip lists: a probabilistic alternative to balanced trees,即跳表。
众所周知,AVL 树的查询时间复杂度严格为 O(logN),但节点插入过程中需要多次旋转,会导致插入效率降低。后来出现的红黑树解决了节点插入的效率问题,但由于其在更新节点时需要多节点参与自身的平衡过程,故在并发场景时就需锁住更多的节点,使得并发效率降低。而 SkipList 由于实现简单,在更新数据时所需参与的节点较少,在并发场景应用较广,比如 Redis 和 Google 的 BigTable。
2. 定义 Skip_list 在 wikipedia 的描述为”a skip list is a probabilistic data structure that allows O(logN) search complexity as well as O(logN) insertion complexity within an ordered sequence of n elements. “,即跳表是一种概率数据结构,它在 n 个元素的有序序列中实现了 O(logN) 的查询复杂度和 O(logN) 的插入复杂度。
3. 原理
不同于一般单链表各节点只有 1 个 next 指针,SkipList 各节点有 x 个 next 指针(x 为随机生成),且这 x 个 next 指针还有“层级概念”
如上图所示,跳表在递增链表各节点的第 i/x 层 next 指针(1 <= i <= x),记录了后续首个层数不低于 i 的节点的地址。
查询时从首节点顶层开始查找:
(若本层 next 指向节点的值为空,未找到且无跳转节点,则降层继续查找)
(若本层 next 指向节点的值等于目标值,则查询结束,找到)
若本层 next 指向节点的值小于目标值,则跳到指向节点继续查找,而中间层数较矮的节点会被“跳过”(因为链表递增,中间节点一定也小于目标值,故可跳过),从而缩小查询范围
若本层 next 指向节点的值大于目标值,则降层继续查找(因为链表递增,next 指向节点的后续节点一定也大于目标值,故可通过降层排除后续节点),从而缩小查找范围
4. 数据结构设计 由上述 SkipList 原理可知其查询主要围绕节点的 x 层 next 指针,后续的增删改也是建立在此基础上,故这 x 层 next 指针数据结构的实现非常关键。首先需要一个成员变量来记录节点具有多少 next 指针(节点层数 x),其次考虑到层数 x 需要随机生成,故将 next 指针变量设计为双重指针,然后再加上传统单链表的 K,V 成员变量即可(为了方便扩展复用,博主这里采用了模板类实现),具体数据结构如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 template <typename K, typename V>class Node {friend class SkipList <public : Node (); Node (int level); Node (K key, V val, int level); ~Node (); bool operator <(const Node<K, V>& another); private : inline void init_next_nodes (int level) private : int _level; K _key; V _val; Node<K, V>** _next_nodes; };
而 SkipList 对象的数据结构设计则较为简单:一个首节点变量、一个记录对象最大生成层数变量及一个记录节点个数变量即可,支持的方法除增删改查外增加了随机生成层数方法,备份加载 SkipList 对象数据方法,及一个图形化打印方法,具体数据结构如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 template <typename K, typename V>class SkipList {public : SkipList (); ~SkipList (); Node<K, V>* find(const K key); // 查找位置(未找到,得到其上一个位置) bool insert (K key, V val, int level = -1 ) bool del (K key) V* get (K key) ; bool dump (std::string file_path_to_dump = DEFAULT_DUMP_FILE_PATH) bool load (std::string file_path_to_load = DEFAULT_DUMP_FILE_PATH) void graphical_print (void ) std::vector<std::string> stringSplit (const std::string& str, char delim) ; private : inline int gen_rand_Level () private : Node<K, V>* _pre_header; unsigned int _node_cnt; int _max_level; };
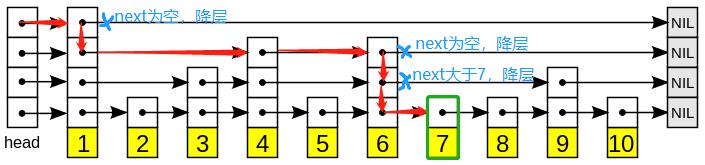
5. 编码实现 5.1. 查询 如上图所示,查询节点 key 为 7 的步骤如下:
以首节点顶层起,此时层数为 4 且本层 next 指针指向节点的 key 为 1(小于目标 7),则跳转到 next 指向的 1 节点
此时在 1 节点 4 层,本层 next 指针指向节点为空,降层
此时在 1 节点 3 层,本层 next 指针指向节点的 key 为 4(小于目标 7),则跳转到 next 指向的 4 节点
此时在 4 节点 3 层,本层 next 指针指向节点的 key 为 6(小于目标 7),则跳转到 next 指向的 6 节点
此时在 6 节点 3 层,本层 next 指针指向节点为空,降层
此时在 6 节点 2 层,本层 next 指针指向节点的 key 为 9(小于目标 7),降层
此时在 6 节点 1 层,本层 next 指针指向节点的 key 为 7(找到)
查询方法实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 template <typename K, typename V>Node<K, V>* SkipList<K, V>::find (const K key) { Node<K, V>* node_ptr = _pre_header; while (node_ptr) { int level_i = node_ptr->_level - 1 ; for (; level_i >= 0 ; --level_i) { if (!node_ptr->_next_nodes[level_i]) { continue ; } if (node_ptr->_next_nodes[level_i]->_key == key) { return node_ptr->_next_nodes[level_i]; } else if (node_ptr->_next_nodes[level_i]->_key < key) { node_ptr = node_ptr->_next_nodes[level_i]; break ; } } if (level_i == -1 ) { break ; } } return nullptr ; }
5.2. 新增节点 如上图插入的动图所示,新增节点的过程大致可分为两步:第一步是与上文查找类似的需要先“查找”到节点的拟插入位置,找到其前后节点、第二步是插入节点后根据其“层高”更新相关节点的第 1 到 x 层 next 指针指向(这里可通过事先记录其查找走过的节点层级“路径”,然后根据记录值找到应该修改哪部分 next 指针),具体编码实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 template <typename K, typename V>bool SkipList<K, V>::insert (K key, V val, int level) { Node<K, V>* record_find_path[MAX_LEVEL] = {nullptr }; Node<K, V>* cur_ptr = _pre_header; for (int level_i = cur_ptr->_level - 1 ; level_i >= 0 ; --level_i) { record_find_path[level_i] = cur_ptr; if (!cur_ptr->_next_nodes[level_i]) { continue ; } if (cur_ptr->_next_nodes[level_i]->_key == key) { cur_ptr->_next_nodes[level_i]->_val = val; return true ; } else if (cur_ptr->_next_nodes[level_i]->_key < key) { cur_ptr = cur_ptr->_next_nodes[level_i]; ++level_i; } } Node<K, V>* gen_node = new Node<K, V>(key, val, level > 0 ? level : gen_rand_Level ()); assert (gen_node); log_debug ("gen node(%s) success, level = %d\n" , std::to_string (gen_node->_key).c_str (), gen_node->_level); for (int level_i = gen_node->_level - 1 ; level_i >= 0 ; --level_i) { if (level_i < _max_level && record_find_path[level_i]) { gen_node->_next_nodes[level_i] = record_find_path[level_i]->_next_nodes[level_i]; } if (level_i < _max_level) { record_find_path[level_i]->_next_nodes[level_i] = gen_node; } else { _pre_header->_next_nodes[level_i] = gen_node; } } ++_node_cnt; if (gen_node->_level > _max_level) { _max_level = gen_node->_level; _pre_header->_level = _max_level; } return true ; }
5.3. 删除节点 与上文新增过程类似,删除节点也可大致分为查询和更新删除后相关 next 指针两步,不过需要注意两点,一是可能存在待删除节点不存在的情况(层数为 0 及时退出)、以及删除节点可能为“最高节点”还调整最大层层数,具体编码实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 template <typename K, typename V>bool SkipList<K, V>::del (K key) { Node<K, V>* record_find_path[MAX_LEVEL] = {nullptr }; Node<K, V>* cur_ptr = _pre_header; Node<K, V>* target_node_ptr = nullptr ; for (int level_i = cur_ptr->_level - 1 ; level_i >= 0 ; --level_i) { record_find_path[level_i] = cur_ptr; if (!cur_ptr->_next_nodes[level_i]) { continue ; } if (cur_ptr->_next_nodes[level_i]->_key == key) { if (!target_node_ptr) { target_node_ptr = cur_ptr->_next_nodes[level_i]; } } else if (cur_ptr->_next_nodes[level_i]->_key < key) { cur_ptr = cur_ptr->_next_nodes[level_i]; ++level_i; } } if (!target_node_ptr) { return false ; } while (_max_level > 0 && _pre_header->_next_nodes[_max_level - 1 ] == target_node_ptr) { _pre_header->_next_nodes[_max_level - 1 ] = target_node_ptr->_next_nodes[_max_level - 1 ]; if (target_node_ptr->_next_nodes[_max_level - 1 ]) { break ; } _pre_header->_level = --_max_level; } for (int level_i = 0 ; level_i < target_node_ptr->_level; ++level_i) { record_find_path[level_i]->_next_nodes[level_i] = target_node_ptr->_next_nodes[level_i]; } delete target_node_ptr; target_node_ptr = nullptr ; --_node_cnt; return true ; }
5.4. 备份 备份一个 SkipList 对象的关键在于记录其每个节点随机生成的层数,博主实现较简单,是通过简单地按照 key,level,value 固定格式将各节点逐行存入文件中,详细实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 template <typename K, typename V>bool SkipList<K, V>::dump (std::string file_path_to_dump) { Node<K, V>* ptr = nullptr ; std::ofstream ofs; ofs.open (file_path_to_dump, std::ios::out | std::ios::trunc); if (!ofs.is_open ()) { log_error ("Open file failed!" ); return false ; } ptr = _pre_header->_next_nodes[0 ]; while (ptr) { ofs << ptr->_key << DELIMITER << ptr->_level << DELIMITER << ptr->_val << std::endl; ptr = ptr->_next_nodes[0 ]; } ofs.close (); return true ; }
5.5. 加载 加载过程是备份的逆向,只需逐行读取并按序解析到对应的 key,level,value 三个值,然后调用 insert() 函数添加即可,由于唯一的随机变量 level 以固定,故可重新生成与备份前结构相同的 SkipList 对象,详细实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 template <typename K, typename V>bool SkipList<K, V>::load (std::string file_path_to_load) { if (access (file_path_to_load.c_str (), F_OK ) != FILE_EXIST) { log_error ("Loading file is not exist!" ); return false ; } std::ifstream ifs; std::string line; ifs.open (file_path_to_load, std::ios::in); if (!ifs.is_open ()) { log_error ("Open file failed!" ); return false ; } while (std::getline (ifs, line)) { std::vector<std::string> elems = stringSplit (line, DELIMITER); if (elems.size () != 3 ) { continue ; } int key = std::stoi (elems[0 ]); int level = std::stoi (elems[1 ]); std::string val = elems[2 ]; insert (key, val, level); } ifs.close (); return true ; }
5.6. 可视化打印 通过由顶向下、由左至右的逐层打印的方式,以直观地显示 SkipList 对象的内容
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 template <typename K, typename V>void SkipList<K, V>::graphical_print () { Node<K, V>* ptr = nullptr ; static const int PRINT_WIDTH = 7 ; if (_node_cnt <= 0 ) { return ; } log_info ("graphical print:\n" ); for (int level_i = _max_level - 1 ; level_i >= 0 ; --level_i) { std::cout << std::right << std::setw (PRINT_WIDTH) << "->" + std::to_string (_pre_header->_next_nodes[level_i]->_key) + " |:" ; ptr = _pre_header->_next_nodes[0 ]; while (ptr) { if (ptr->_level > level_i) { std::cout << std::right << std::setw (PRINT_WIDTH) << ptr->_key; if (ptr->_next_nodes[level_i]) { std::cout << std::left << std::setw (PRINT_WIDTH) << " (->" + std::to_string (ptr->_next_nodes[level_i]->_key) + ")" ; } } else { std::cout << std::right << std::setw (PRINT_WIDTH * 2 ) << " " ; } ptr = ptr->_next_nodes[0 ]; } std::cout << std::endl; } std::cout << std::endl; }
可视化打印效果如下: