B+树与B*树
1. B+树
1.1. B+树简介
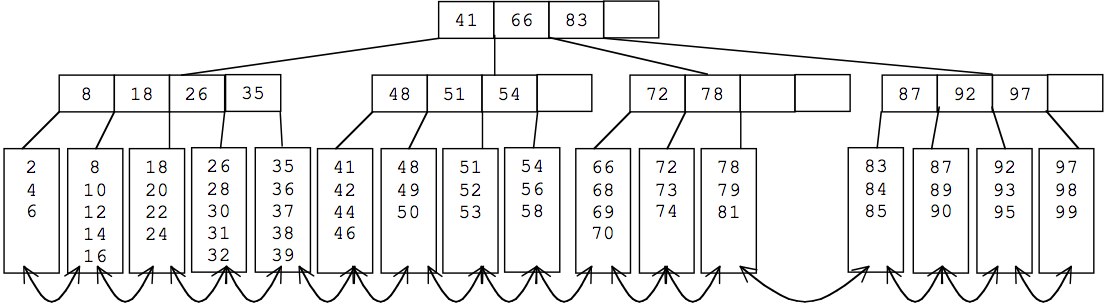
B+树是一种树数据结构,是一个n叉树,每个节点通常有多个孩子,一棵B+树包含根节点、内部节点和叶子节点。根节点可能是一个叶子节点,也可能是一个包含两个或两个以上孩子节点的节点。
1.2. B+树应用场景
B+树通常用于数据库和操作系统的文件系统中。NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和BFS等文件系统都在使用B+树作为元数据索引。B+树的特点是能够保持数据稳定有序,其插入与修改拥有较稳定的对数时间复杂度。B+树元素自底向上插入。
1.3. B+树定义
- B+树是应文件系统所需而出的一种B树的变型树。一棵m阶的B+树和m阶的B树的差异在于:
- 有n棵子树的结点中含有n个关键字,每个关键字不保存数据,只用来索引,所有数据都保存在叶子节点。
- 所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的非终端结点可以看成是索引部分,结点中仅含其子树(根结点)中的最大(或最小)关键字。
备注:通常在B+树上有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点。
- B+树是B树的变体,也是一种多路搜索树,其定义除以下存有差异的定义外基本与B树同:
- 非叶子结点的子树指针与关键字个数相同;
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B树是开区间);
- 为所有叶子结点增加一个链指针;
- 所有关键字都在叶子结点出现;
备注:B+的搜索与B树也基本相同,区别是B+树只有达到叶子结点才命中(B树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
1.4. B+的特性
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
- 不可能在非叶子结点命中;
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
- 更适合文件索引系统;
2. B*树
2.1. B*树的定义
- 是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;
- B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2);
3. B树,B+树,B*树小结
| 数据结构 | 小结 |
|---|---|
| B树 | 多路搜索树,每个结点存储M/2到M个关键字,非叶子结点存储指向关键字范围的子结点;所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中; |
| B+树 | 在B树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中; |
| B*树 | 在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3; |
4. B树,B+树与B*树的优缺点比较
备注:B-树就是B树,”-“是个连字符号,不是减号。
4.1. B树 vs B+树
- B树是一种平衡的多路查找(又称排序)树,在文件系统中有所应用。主要用作文件的索引。其中的B就表示平衡(Balance)
- B+树有一个最大的好处,方便扫库,B树必须用中序遍历的方法按序扫库,而B+树直接从叶子结点挨个扫一遍就完了。
- B+树支持range-query(区间查询)非常方便,而B树不支持。这是数据库选用B+树的最主要原因。比如要查 5-10之间的,B+树一把到5这个标记,再一把到10,然后串起来就行了,B树就非常麻烦。B树的好处,就是成功查询特别有利,因为树的高度总体要比B+树矮。不成功的情况下,B树也比B+树稍稍占一点点便宜。
- B树的优势是当你要查找的值恰好处在一个非叶子节点时,查找到该节点就会成功并结束查询,而B+树由于非叶节点只是索引部分,这些节点中只含有其子树中的最大(或最小)关键字,当非终端节点上的关键字等于给点值时,查找并不终止,而是继续向下直到叶子节点。因此在B+树中,无论查找成功与否,都是走了一条从根到叶子节点的路径。有很多基于频率的搜索是选用B树,越频繁query的结点越往根上走,前提是需要对query做统计,而且要对key做一些变化。
- 另外B树也好B+树也好,根或者上面几层因为被反复query,所以这几块基本都在内存中,不会出现读磁盘IO,一般已启动的时候,就会主动换入内存。 mysql底层存储是用B+树实现的,因为内存中B+树是没有优势的,但是一到磁盘,B+树的威力就出来了。
4.2. B+树 vs B*树
- B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;B树定义了非叶子结点关键字个数至少为(2/3)M,即块的最低使用率为2/3(代替B+树的1/2);
- B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
- B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针; 所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
5. 参考文档
相关文章