基于C++的B树的数据结构设计与编码实现
1. B树的原理及性能
1.1. 定义
1970年,R.Bayer和E.mccreight提出了一种适用于外查找的树,它是一种平衡的多叉树,称为B树。
一棵m阶B树是一棵平衡的m路搜索树。当m取2时,就是我们常见的二叉搜索树。它或者是空树,或者是满足下列性质的树:
- 根结点至少有两个子女;
- 每个非根节点所包含的关键字个数 j 满足:┌m/2┐ - 1 <= j <= m - 1;(┌,向上取整)
- 除根结点以外的所有非叶子结点的度数正好是关键字总数加1;故内部子树个数 k 满足:┌m/2┐ <= k <= m ;
- 所有叶子节点都位于同一层
备注:
- 每个结点中关键字从小到大排列,并且当该结点的孩子是非叶子结点时,该k-1个关键字正好是k个孩子包含的关键字的值域的分划
- 叶子结点的数目正好等于树中所包含的关键字总个数加1
- B-树中的一个包含n个关键字,n+1个指针的结点的一般形式为: (n,P0,K1,P1,K2,P2,…,Kn,Pn)
1.2. B树的查询性能
设B树包含N个关键字,有N+1个叶子节点。B树高为:1 + log┌m/2┐((N+1)/2 ),(叶子节点层不在计算内),每次查询只需要┌m/2┐的对数时间,当m>2时查询效率优于二叉搜索树,故B树数据结构具备较高的查询性能。
2. 基于C++实现B树能带来哪些优势?
- 设计数据结构时,可采用面向对象设计思路,可根据数据特征灵活自定义每个 BTree 对象的阶数 m
- 可利用C++的模板类进行设计,可在实例化时自定义 <KEY_TYPE, VALUE_TYPE> 的具体类型
- 具备面向对象设计的传统优势:易维护、质量高、效率高、易扩展
3. B树的数据结构设计
由B树的定义可知它是一种多叉树的结构,而组成多叉树的基本单位为节点(中间节点、叶子节点),故实现B数的数据结构设计的关键点在于对B树节点的设计
3.1. B树节点的数据结构设计
3.1.1. 最大m-1个关键字及m个关键字对应值的存放

在一个m阶的B树(多叉树)中,每个节点最多包含m-1个关键字及m个关键字指向的值。其中关键字指向的值可能非值的地址(依然为中间节点的地址),则该关键字对应的值采取逐层下放到下一节点Ptr0所指向的值(可能依然为中间节点),直至叶子节点Ptr0指向的值;同理,其他关键字:Key0 ~ Key(m-2)对应的值为:Ptr1 ~ Ptr(m-1),若非叶子节点则逐层下放直至叶子节点的Ptr0所指向的值。
考虑到不是每个节点都存满m-1个关键字,故还需要一个变量记录当前节点已有关键字数。尽管可以通过遍历Ptrs1~Ptr(m-1),统计为NULL的个数cnt,从而得到已有关键字数:m - 1 - cnt,但当m阶数过大(实际应用阶数m一般大于100)时,浪费很多不必要的CPU资源计算现有关键字数,故采用4字节int直接记录当前节点所包含关键字数
对于中间节点,其Ptrs指针指向的子节点可能为:叶子节点或中间节点,故还需要一个bool值来记录当前节点指向的是叶子节点还是中间节点
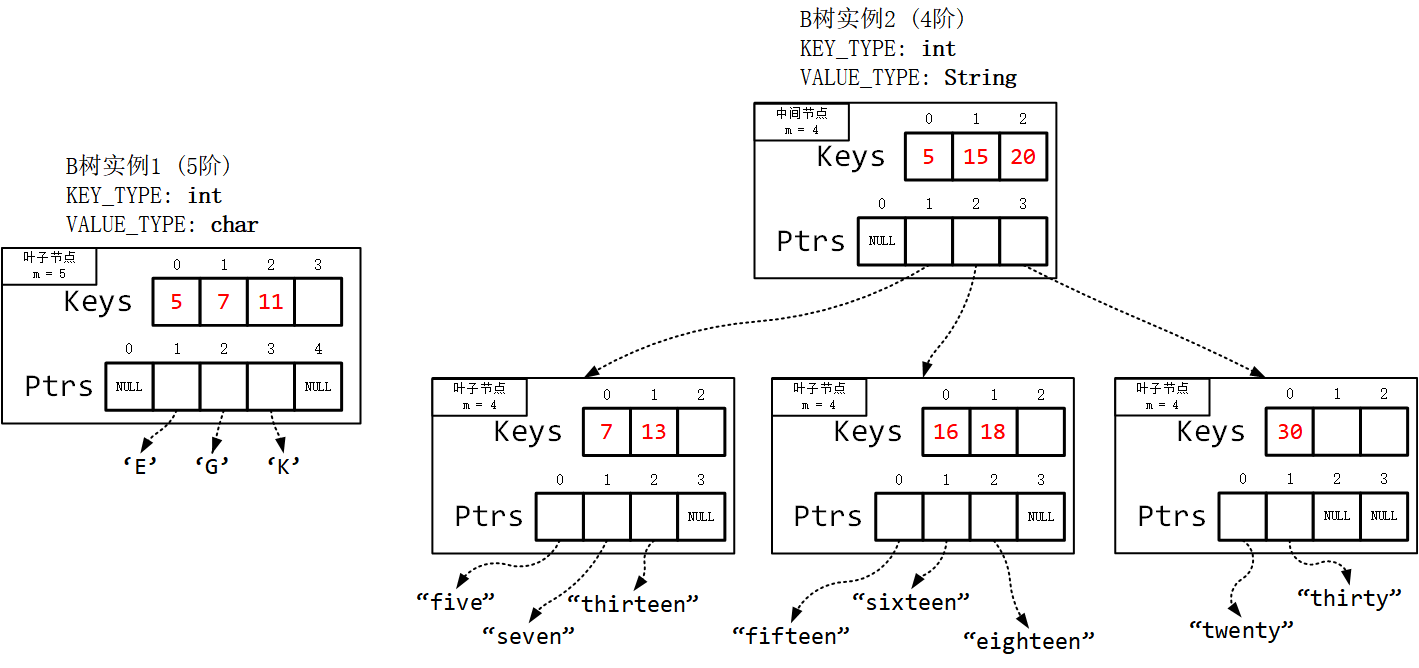
分析至此可知,只需对叶子节点类定义:包含关键字数变量和两成员数组变量: 关键字数组KEY_TYPE[m - 1]、值指针数组VALUE_TYPE[m];中间节点类定义:指向的下一节点是否是叶子节点、包含关键字数变量和两成员数组变量:关键字数组KEY_TYPE[m - 1]、子节点指针数组BTreeNode*[m]
1 | // 叶子节点类 |
3.1.2. 优化:融合叶子节点类和中间节点类
比较叶子节点类与中间节点类易知,其大多数成员变量相同,为简化后续管理节点类管理及后续中间节点与叶子节点相互转换,尝试将叶子节点类与中间节点类融合。采用一个bool值(isLeaf)记录当前节点是否是叶子节点,则中间节点类的指向子节点类型(原: isChildLeafNode)可通过判断子节点的isLeaf的bool值判断。
进一步优化。叶子节点类的指向value的指针数组VALUE_TYPE*[m]与中间节点的指向下一节点子节点指针数组BTreeNode*[m]所占内存一致,且互斥不可能在融合类中同时使用这两个数组,故采用union使这两个数组复用同一块内存以节省内存开销。
1 | template<class KEY_TYPE, class VALUE_TYPE> |
- 至此,存储节点信息已基本完成。但由于后续分裂节点,维持节点平衡需要用到该节点的父节点信息,若从根节点开始向下遍历较浪费CPU资源和时间开销,故在每个节点增加记录其父节点地址的指针变量parent,最终B树节点类的数据结构如下:
1 | template<class KEY_TYPE, class VALUE_TYPE> |
3.2. B树管理类的数据结构设计
相比于B树节点类,B数管理类的数据结构则相对简单:维护3个变量分别记录该实例的阶数(m),最少关键字数(minKeyNum),最多关键字个数(maxKeyNum)以及根节点(root)便可,其数据结构如下:
1 | class BTree { |
4. B树支持的操作及编码实现
4.1. 实例化一个m阶的B树实例

- 实例化BTree,申请BTree类所需内存,根据输入的阶数m初始化成员变量: 阶数(m),最少关键字数(minKeyNum),最多关键字个数(maxKeyNum)
- 实例化一个B树节点BTreeNode作为根节点(根节点为叶子节点),初始化BTreeNode成员变量,并根据此实例化B树的阶数申请关键字数组keys 和 指向value的指针数组valuePtrs所需内存。
1 | /** |
4.2. 释放一个m阶的B树实例
释放BTree实例,会调用BTree类的析构函数释放普通类型的成员变量和B树节点BTreeNode指针(root)指向的内存。
释放BTreeNode实例(eg. root),会调用BTreeNode类的析构函数释放普通类型的成员变量,手动申请的关键字数组keys,会根据当前节点是否是叶子节点遍历释放申请的value的指针数组或遍历并递归释放中间节点的子节点指针数组指向的内存。
1 | /** |
4.3. 二分法查询关键字
在一个m阶的B树(多叉树)中,每个节点最多包含m-1个关键字(实际使用为减少层高,一般m会较大eg. m > 100),且这些关键字严格递增。从根节点开始查询某key时,若只是采用从左至右线性遍历节点的关键字数组将浪费较多的Cpu资源:O(m),且没有利用好严格递增的特性,故在查询关键字时,一般采用二分法以减少每个节点检索关键字时间:O(log(m))。
由于B树满足二叉搜索树特性(值:右 < 根 < 左),在从根节点开始查询关键字时,若无法在本节点找到关键字 k,则k有可能在以本节点**不超过k关键字**指向节点为根的子树中(此节点非叶节点),故搜索关键字可简化为:对当前节点,返回keys[i] >= key对应的子节点可能所在下标 i,外层判断keys[i] 的值与key,直至找到key,或下降至叶子节点都未找到。
4.3.1. 对每个节点,二分法返回第一个 keys[i] >= key 的下标 i
其中,返回当前节点第一个 keys[i] >= key 对应的子节点可能所在下标 i 伪代码如下:
- 若本节点若无关键字且非叶子节点,则返回下标0
- 二分法找到不超过 key 值所对应的下标 i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23/**
* 二分查询关键字数组中,第一个keys[i] >= key对应的子节点可能所在下标 i
* @tparam KEY_TYPE
* @tparam VALUE_TYPE
* @param key
* @return i -- 可能的子节点下标
*/
template<class KEY_TYPE, class VALUE_TYPE>
int BTreeNode<KEY_TYPE, VALUE_TYPE>::binarySearchKey(KEY_TYPE key) {
if (keyNum <= 0) {
return 0;
}
int left = 0, right = keyNum - 1, mid = (left + right) / 2;
while (left < right && keys[mid] != key) {
if (keys[mid] > key) {
right = mid - 1;
} else {
left = mid + 1;
}
mid = (left + right) / 2;
}
return key > keys[mid] ? mid + 1 : mid;
}
4.3.2. 外层二分查询关键字key
外层判断keys[i] 的值与key,若keys[i] 不等于 key,若非叶子节点,则将查找任务下降为子节点childPtrs[i]查找key,若直至叶子节点都未找到,则返回nullptr;若 keys[i] 等于 key,但此时节点非叶子节点,则依次下降遍历子节点的第0个指针数组指向的子节点,直至叶子节点ptr->valuePtrs[0]即为 key 对应值的指针。
1 | /** |
4.4. 插入<key, value>键值对
由于m阶的B树(多叉树)中,每个节点最多包含m-1个关键字(有限),故插入<key, value>键值对前,需判断待插入节点的关键字剩余容量后操作:若非零(未满插入),直接填充<key, value>到已有的keys数组尾部即可;若为零(已满插入),需要对节点进行分裂操作,为加速插入过程,博主实现时将节点分裂和插入融合为一个操作分裂插入。
4.4.1. 先找到要插入该key的节点
- 从根节点开始,查找key
- 若key已存在,则只需下降到叶节点,将其value指针指向新value地址即可
- 若向下搜索到叶节点都未找到key,则该叶子节点即为我们要插入<key, value>键值对的节点
4.4.2. 未满节点插入<key, value>键值对

对于节点关键字节点未满插入,只需将新的<key, value>键值对对应插入尾部即可。
4.4.3. 已满节点插入<key, value>键值对

对于关键字已满的节点,需新增右兄弟节点,将原已满节点的后半部分挪到右兄弟节点(“分裂”),会上升一个key到其父节点作为新增右兄弟节点对应的key(若无则创建新父节点),再插入新节点。博主这里将这两步操作(分裂 + 插入)合为一步以提高效率:
- 新增右兄弟节点 rightBrotherPtr
- 下标变换以模拟过载1插入该key后的数组分裂
- 记录模拟过载1后的数组对应 midKey,作为新增右兄弟节点在父节点的key值<midKey, rightBrotherPtr>
- 将 midKey 之后的后半部分key及其对应valuePtr挪到右兄弟节点
- 刷新分裂后两兄弟节点的关键字容量 keyNum 的数值
- 最后将新增的右兄弟节点和其对应的Key值: <rightBrotherKey, rightBrotherPtr>,插入共同的父节点(无父节点则需新增父节点/root节点)
4.5. 删除<key, value>键值对
- 对于<key, value>键值对的删除,若B树中查无该key,则不多讨论直接返回false。由于所有的记录valuePtr的指针数组都在叶子节点层,若在叶子节点查到该key,则还好,若在中间节点查到该key,意味着该key对应的value的地址记录在其子树下降直至叶子节点层的第0个元素内,对该key删除后,若子树非空,还需在最初找到该key的位置补充一个key作为新子树的key。
- B树作为一颗m阶搜索树,存在搜索树的缺陷——退化为链表的,另一方面为了降低层高,B树还要求了每个节点的最少关键字数(m/2, m阶),以保证查询效率,若删除键值对后发现关键字数小于m/2,还需进行一系列平衡操作。
4.5.1. 删除<key, value>键值对 (假设删除后 keyNum > m/2,无需考虑平衡)

- 若此节点非叶子节点,记录该key地址recordKey,继续下落到叶子节点执行删除(若子树非空,需更新整个子树的key,若子树为空,还需递归上层删除)
- 若下落的到叶子节点,关键字数为0,释放该叶子节点,并执行递归向上删除
- 若下落到叶子节点,关键字数非0,则截取下一个key以更新recordKey,删除叶子节点对应的valuePtr值,其他key及对应记录的value地址前挪。
4.6. 删除<key, value>键值对后的平衡操作
4.6.1. 尝试从左、右兄弟节点挪借关键字

- 若无左(或右)兄弟节点,或左右节点无法提供可挪借关键字,则挪借失败
- 若存在左(或右)兄弟节点 且 左(或右)兄弟节点关键字字数大于 minKeyNum,则可从左(或右)兄弟挪借关键字
- 若左、右兄弟节点均可挪借关键字数,从平衡角度选择可挪借关键字数较多的一方挪借
4.6.2. 尝试与左或右兄弟节点合并

- 若存在左兄弟节点,且左兄弟节点关键字 + 本节点关键字 + 1 <= 最大关键字数,则可与左兄弟节点合并
- 若存在右兄弟节点,且右兄弟节点关键字 + 本节点关键字 + 1 <= 最大关键字数,则可与右兄弟节点合并
- 若左、右兄弟节点均不可合并,则返回合并失败
- 若均可合并,选取左右兄弟节点中,从平衡角度选择关键字数较少的一方合并
4.6.3. 若节点的关键词数为0,且非叶子节点(降层)

- 若当前节点关键字数大于0,或为叶子节点,不进行降层
- 若其兄弟节点与其node->childPtrs[0] 是否是叶子节点属性不同,则不降层
- 降层处理,将其父节点指向其的childPtrs[i]指针,指向其node->childPtrs[0]指向的值,后释放node节点
- 若该节点为根节点,则将root指针指向node->childPtrs[0](更新root节点),清除父节点指向node指针的值后释放node节点
4.7. 更多详细的实现细节,请阅读我上传到Git的源码吧:)
博主基于C++的B树的数据结构设计与编码实现源码详见:
https://github.com/haoleeson/Cpp_Learning/blob/master/myBTree.h