![]()
排序作为常用的解决实际问题的计算方法,被广泛应用于生活中的方方面面。而处理实际问题的数据规模常常十分庞大,同一个计算任务选用不同的算法,其执行效率可能相差几百倍,几千倍甚至更高,因此效率常被作入为评判一个算法优劣的重要指标。
博主对七种常见的排序算法进行编码实现,和以处理同规模数据所耗时长为指标进行了性能比较(冒泡、选择、插入、希尔、堆、归并和快排)。
1. 测试排序函数运行时间方法
运行排序算法前后打点,取前后两次打点的差值,再除以打点的频率得到函数的运行时长。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
double SortFuncCompare::testRunTime(void (*pFunction)(ElementType *)) {
clock_t start, stop;
double runTime;
start = clock();
(*pFunction)(m_array);
stop = clock();
runTime = ((double)stop - (double)start) / CLOCKS_PER_SEC;
return runTime;
}
|
2. 测试函数
定义排序函数的函数指针数组,size为7,逐一将七种static函数地址赋值到函数指针数组,然后循环执行七种函数对相同规模的随机数组的排序操作,便可得到各排序算法在各规模数据下的运行时长。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| void (*func[NUM_OF_SORT_FUNC])(ElementType*);
func[0] = Bubble_Sort;
func[1] = Selection_Sort;
func[2] = Insertion_Sort;
func[3] = Shell_Sort;
func[4] = Heap_Sort;
func[5] = Merge_Sort;
func[6] = Quick_Sort;
void SortFuncCompare::testFuncRuntime(void) {
double *runTime = new double[NUM_OF_SORT_FUNC];
for (unsigned int size = MIN_NUM_OF_RAND_ARRAY; size <= MAX_NUM_OF_RAND_ARRAY; size *= 10) {
for (int i = 0; i < NUM_OF_SORT_FUNC; ++i) {
refreshArray(size);
*(runTime + i) = testRunTime(func[i]);
}
cout << "Num of Array = " << size << "\t: ";
for (int j = 0; j < NUM_OF_SORT_FUNC - 1; ++j) {
cout << *(runTime + j) << ", ";
}
cout << *(runTime + NUM_OF_SORT_FUNC - 1) << endl;
}
delete[] runTime;
}
|
3. 七种经典排序算法的C++编码实现
3.1. 冒泡排序
时间复杂度:O(N^2),空间复杂度:O(1),原地,稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void SortFuncCompare::Bubble_Sort(ElementType* pArray) {
bool swapFlag;
for (int i = m_uiSizeOfArray - 1; i > 0; --i) {
swapFlag = false;
for (int j = 0; j < i; ++j) {
if (*(pArray + j) COMPARE *(pArray + j + 1)) {
swapTwoNum(pArray + j, pArray + j + 1);
if (!swapFlag)
swapFlag = true;
}
}
if (!swapFlag)
break;
}
}
|
3.2. 选择排序
时间复杂度:O(N^2),空间复杂度:O(1),原地,稳定
1
2
3
4
5
6
7
8
9
| void SortFuncCompare::Selection_Sort(ElementType *pArray) {
for (int i = 0; i < m_uiSizeOfArray - 1; ++i) {
for (int j = i + 1; j < m_uiSizeOfArray; ++j) {
if (*(pArray + i) COMPARE *(pArray + j))
swapTwoNum(pArray + i, pArray + j);
}
}
}
|
3.3. 插入排序
时间复杂度:O(N^2),空间复杂度:O(1),原地,稳定
1
2
3
4
5
6
7
8
9
10
11
12
| void SortFuncCompare::Insertion_Sort(ElementType *pArray) {
ElementType tmp;
int j;
for (int i = 1; i < m_uiSizeOfArray; ++i) {
tmp = *(pArray + i);
for (j = i; j > 0 && *(pArray + j - 1) COMPARE tmp; --j) {
*(pArray + j) = *(pArray + j - 1);
}
*(pArray + j) = tmp;
}
}
|
3.4. 希尔排序
时间复杂度:O(N^1.25 ~N^1.5),空间复杂度:O(1),原地,非稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void SortFuncCompare::Shell_Sort(ElementType *pArray) {
ElementType tmp;
int j;
for (int D = m_uiSizeOfArray / 2; D > 0; D /= 2) {
for (int i = D; i < m_uiSizeOfArray; ++i) {
tmp = *(pArray + i);
for (j = i; j >= D && *(pArray + j - D) COMPARE tmp; j -= D) {
*(pArray + j) = *(pArray + j - D);
}
*(pArray + j) = tmp;
}
}
}
|
3.5. 堆排序
时间复杂度:O(NlogN),空间复杂度:O(1),原地,非稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| void SortFuncCompare::Heap_Sort(ElementType *pArray) {
for (int i = m_uiSizeOfArray / 2 - 1; i >= 0; --i) {
heapDown(pArray, i, m_uiSizeOfArray);
}
for (int j = m_uiSizeOfArray - 1; j >= 1; --j) {
swapTwoNum(pArray, pArray + j);
heapDown(pArray, 0, j);
}
}
void SortFuncCompare::heapDown(ElementType *pArray, int fatherIndex, int maxIndex) {
int sonIndex = 2 * fatherIndex + 1;
if (sonIndex < maxIndex) {
if (sonIndex + 1 < maxIndex && *(pArray + sonIndex + 1) COMPARE *(pArray + sonIndex))
++sonIndex;
if (*(pArray + sonIndex) COMPARE *(pArray + fatherIndex))
swapTwoNum(pArray + sonIndex, pArray + fatherIndex);
heapDown(pArray, sonIndex, maxIndex);
}
}
|
3.6. 归并排序
时间复杂度:O(NlogN), 空间复杂度:O(n),非原地,非稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| void SortFuncCompare::Merge_Sort(ElementType *pArray) {
ElementType* tmpA = new ElementType[m_uiSizeOfArray];
if (NULL != tmpA) {
mergeSort(pArray, tmpA, 0, m_uiSizeOfArray - 1);
delete[] tmpA;
}
}
void SortFuncCompare::mergeSort(ElementType *pArray, ElementType *tmpA, int leftIndex, int rightIndex) {
if (leftIndex < rightIndex) {
int middleIndex = (leftIndex + rightIndex) / 2;
mergeSort(pArray, tmpA, leftIndex, middleIndex);
mergeSort(pArray, tmpA, middleIndex + 1, rightIndex);
merge(pArray, tmpA, leftIndex, middleIndex + 1, rightIndex);
}
}
void SortFuncCompare::merge(ElementType *pArray, ElementType *tmpA,
int leftIndex, int middleIndex, int rightIndex) {
int leftSubIndex = leftIndex;
int rightSubIndex = middleIndex;
int tmpIndex = leftIndex;
while (leftSubIndex < middleIndex && rightSubIndex <= rightIndex) {
*(tmpA + tmpIndex++) = (*(pArray + leftSubIndex) COMPARE *(pArray + rightSubIndex)) ?
*(pArray + rightSubIndex++) : *(pArray + leftSubIndex++);
}
while (leftSubIndex < middleIndex) {
*(tmpA + tmpIndex++) = *(pArray + leftSubIndex++);
}
while (rightSubIndex <= rightIndex) {
*(tmpA + tmpIndex++) = *(pArray + rightSubIndex++);
}
for (int i = leftIndex; i <= rightIndex; ++i) {
*(pArray + i) = *(tmpA + i);
}
}
|
3.7. 快速排序
时间复杂度:O(NlogN ~ N^2),空间复杂度:O(1),原地,非稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| void SortFuncCompare::Quick_Sort(ElementType *pArray) {
quickSort(pArray, 0, m_uiSizeOfArray - 1);
}
#define MIN_NUM_OF_CUTOFF 32
void SortFuncCompare::quickSort(ElementType *pArray, int leftIndex, int rightIndex) {
if (rightIndex - leftIndex > MIN_NUM_OF_CUTOFF) {
int i = leftIndex;
int j = rightIndex - 1;
ElementType middlePivot = choosePivot(pArray, leftIndex, rightIndex);
while(true) {
while (middlePivot COMPARE *(pArray + ++i)) {}
while (*(pArray + --j) COMPARE middlePivot) {}
if (i < j) {
swapTwoNum(pArray + i, pArray + j);
} else {
break;
}
}
swapTwoNum(pArray + i, pArray + rightIndex - 1);
quickSort(pArray, leftIndex, i - 1);
quickSort(pArray, i + 1, rightIndex);
} else {
ElementType tmp;
int j;
for (int i = leftIndex + 1; i <= rightIndex; ++i) {
tmp = *(pArray + i);
for (j = i; j > leftIndex && *(pArray + j - 1) COMPARE tmp; --j) {
*(pArray + j) = *(pArray + j - 1);
}
*(pArray + j) = tmp;
}
}
}
ElementType SortFuncCompare::choosePivot(ElementType *pArray, int leftIndex, int rightIndex) {
int middleIndex = (leftIndex + rightIndex) / 2;
if (*(pArray + leftIndex) COMPARE *(pArray + middleIndex)) {
swapTwoNum(pArray + leftIndex, pArray + middleIndex);
}
if (*(pArray + leftIndex) COMPARE *(pArray + rightIndex)) {
swapTwoNum(pArray + leftIndex, pArray + rightIndex);
}
if (*(pArray + middleIndex) COMPARE *(pArray + rightIndex)) {
swapTwoNum(pArray + middleIndex, pArray + rightIndex);
}
swapTwoNum(pArray + middleIndex, pArray + rightIndex - 1);
return *(pArray + rightIndex - 1);
}
|
4. 时耗测试
各排序算法在各个数据规模下排序所耗时长(秒)。
| 数据规模 |
冒泡 |
选择 |
插入 |
希尔 |
堆 |
归并 |
快排 |
| 十 |
2e-06 |
1e-06 |
1e-06 |
1e-06 |
2e-06 |
1e-06 |
1e-06 |
| 百 |
3.3e-05 |
3.3e-05 |
8e-06 |
8e-06 |
1.1e-05 |
1e-05 |
5e-06 |
| 千 |
0.003153 |
0.003 |
0.000627 |
0.000164 |
0.00016 |
0.000118 |
6.9e-05 |
| 万 |
0.365065 |
0.387825 |
0.060752 |
0.001938 |
0.002096 |
0.001431 |
0.00089 |
| 十万 |
38.2601 |
35.2071 |
7.63559 |
0.034236 |
0.031059 |
0.019387 |
0.01238 |
| 百万 |
9708.16 |
3736.74 |
1643.99 |
0.93 |
0.98 |
0.5 |
0.3 |
4.1. 分析
4.2. 此次实验收获
- 各种排序算法在数规模小于一百时还没有太大差距,此时选实现较简单的就好
- 当数据达到一定规模后,不同算法执行效率差异巨大,此时追求算法效率显得十分重要
5. 附件
本次实验源代码详见博主的个人git仓库:
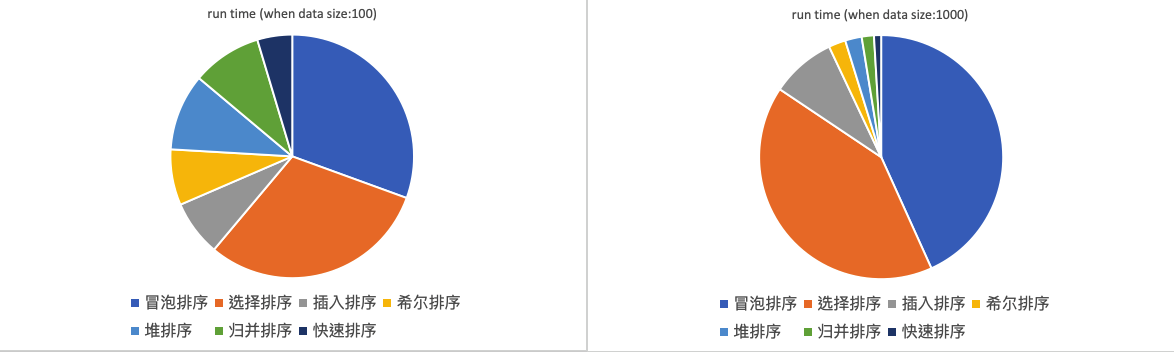
![]() 当数据规模较小时,各排序算法所耗时长区别并不明显,但当数据规模为一百时已有明显区别,最快的排序算法与最满的排序算法效率相差一个数量级。
当数据规模较小时,各排序算法所耗时长区别并不明显,但当数据规模为一百时已有明显区别,最快的排序算法与最满的排序算法效率相差一个数量级。
![]() 除了冒泡和选择排序耗时三十几毫秒,其他排序算法耗时均在一毫秒内,此时各排序算法最快与最满效率比值已达为四十多倍
除了冒泡和选择排序耗时三十几毫秒,其他排序算法耗时均在一毫秒内,此时各排序算法最快与最满效率比值已达为四十多倍
![]() 当排序数据规模达到十万时,可以发现排序最快的算法是快排仅12毫秒,效率是最慢的冒泡排序(38秒)的三千多倍,性能差异已十分明显。
当排序数据规模达到十万时,可以发现排序最快的算法是快排仅12毫秒,效率是最慢的冒泡排序(38秒)的三千多倍,性能差异已十分明显。
 当数据规模较小时,各排序算法所耗时长区别并不明显,但当数据规模为一百时已有明显区别,最快的排序算法与最满的排序算法效率相差一个数量级。
当数据规模较小时,各排序算法所耗时长区别并不明显,但当数据规模为一百时已有明显区别,最快的排序算法与最满的排序算法效率相差一个数量级。
 除了冒泡和选择排序耗时三十几毫秒,其他排序算法耗时均在一毫秒内,此时各排序算法最快与最满效率比值已达为四十多倍
除了冒泡和选择排序耗时三十几毫秒,其他排序算法耗时均在一毫秒内,此时各排序算法最快与最满效率比值已达为四十多倍
 当排序数据规模达到十万时,可以发现排序最快的算法是快排仅12毫秒,效率是最慢的冒泡排序(38秒)的三千多倍,性能差异已十分明显。
当排序数据规模达到十万时,可以发现排序最快的算法是快排仅12毫秒,效率是最慢的冒泡排序(38秒)的三千多倍,性能差异已十分明显。