DBSCAN算法——数据挖掘
1. DBSCAN算法简介
- 基于密度的噪声应用空间聚类(DBSCAN)是Martin Ester,Hans-Peter Kriegel,JörgSander和Xiaowei Xu于1996年提出的数据聚类算法。
- 它是一种基于密度的聚类算法:给定一些空间中的一组点,它将紧密堆积在一起的点(具有许多邻近邻居的点)组合在一起,标记为单独位于低密度区域的离群点(最近的点)邻居们太远了)。
- DBSCAN是最常见的聚类算法之一,也是科学文献中引用最多的算法。
- 2014年,该算法在领先的数据挖掘会议KDD上获得了时间奖的测试(在理论和实践中获得了大量关注的算法奖)。
2. Python编程实现DBSCAN算法
DBSCAN算法主要分为以下步骤实现:
- S1. 任意选择一个未访问过的点 P
- S2. 标记点 P为已访问
- S3. 计算得到所有从p 关于 Eps 和 MinPts 密度可达的点的集合 NeighborPts
- S4. 若 P 不是核心对象,标记点 P 为噪声,跳转步骤S1重新选取 P;若 P 为核心对象,则扩展当前核心对象 P 的所属簇(expandCluster函数)
- S5. 判断是否所有点均已被访问,若是则跳转S6; 若否则继续 S1 ~ S5步骤
- S6. DBSCAN算法运行结束,返回二维分类数组Cluster
3. DBSCAN算法Python代码实现如下
1 | # 基于密度的DBSCAN算法 |
3.1. DBSCAN算法中的关键函数–expandCluster函数实现步骤
- S1. 将当前核心对象 P 添加到新的 P 的所属类Cluster_P中
- S2. 从点 P 的邻域列表 NeighborPts 中取一个点 P’
- S3. 判断点 P’ 是否已被访问。若已被访问,跳转步骤S7;若未被访问,继续执行下一步骤
- S4. 标记点 P’ 为已被访问,并计算得到所有从P’ 关于 Eps 和 MinPts 密度可达的点的集合 NeighborPts_i
- S5. 判断点 P’ 是否为核心对象,若是,将 P’ 的邻域内点 NeighborPts_i 非重复地添加到点 P 的扩展邻域列表NeighborPts中;若否,继续执行下一步骤
- S6. 判断点 P’ 是否已经被分类,若否,添加点 P’ 到列表 Cluster_P 中;若是,继续执行下一步骤
- S7. 判断是否 P 扩展邻域列表 NeighborPts 中的所有元素均已被访问,若否,则循环步骤 S2 ~ S7; 若是,继续执行下一步骤
- S8. 将列表 Cluster_P 添加到总分类列表 Cluster 中
3.2. expandCluster函数Python代码实现如下:
1 | # 扩展当前核心对象 P 的所属簇 |
4. DBSCAN算法执行、参数调整并分析
4.1. 显示聚类前后对比图函数
1 | # 显示聚类前后对比图(最多表示8种颜色的集群) |
4.2. 主函数
1 | # main函数 |
4.3. long.mat文件的DBSCAN算法聚类效果
尝试设置Eps#邻域半径、MinPts#邻域内元素个数(包括点P)两个参数,由于Eps及MinPts两个参数没设置好导致被分成许多类,不方便绘图显示每个类。调试参数时也确认了两个参数设置的重要性,参数对分类结果的影响如下:
Eps=0.08, MinPts=7
当设置Eps=0.08, MinPts=7时已经能够成功绘制图形,但数据被分成6个类,效果不是很理想,如下图所示
分析:虽然能从图中明确看出被分成6个类,但视觉分析应该分成2个类更合适,间接说明分类数过多,表明在扩展其中两个大类时与另外两个类“断开了”,下面分别尝试增加领域半径Eps值、减小MinPts#邻域内元素个数,尝试让小类与大类“连接”起来。
Eps=0.1, MinPts=7
当只增加领域半径Eps值,MinPts不变,设置Eps=0.1, MinPts=7,分类结果如下图所示
分析:增加领域半径Eps值已有明显效果,此时分类数为3,继续尝试增大领域半径Eps值
Eps=0.18, MinPts=7
继续增大Eps值直到Eps=0.18, MinPts=7时才能被分为两类,分类结果如下图所示
分析:虽然此时按密度被成功聚类为2类,但相比之下每个类变得更“松散”,包括了许多不需要的边界非核心对象
Eps=0.08,MinPts=5
当只减小MinPts,领域半径Eps值不变,设置Eps=0.08, MinPts=5时,数据分类数为5,如下图所示
分析:一味只减少MinPts并没有得到很好的聚类结果,尝试减少MinPts并不能实现只分为两类的效果
Eps=0.15,MinPts=8
综合调节Eps邻域半径大小与MinPts邻域内元素个数,设置Eps=0.15, MinPts=8时分类数为2,分类结果如下图所示
分析:联合调整参数Eps和MinPts比只更改单一变量更难调节,在能够分类成2个类的结果下,Eps邻域半径越小、MinPts邻域内元素个数越小,得到的聚类内部对象间隔越“紧密”
4.4. 其他文件数据的DBSCAN聚类结果
由于调整Eps#邻域半径、MinPts#邻域内元素个数参数方法与上面一致,为直观显示效果,只给出聚类较理想的结果图及其对应Eps、MinPts参数
4.4.1. moon.mat文件的DBSCAN算法聚类效果
当设置Eps=0.11, MinPts=5时,数据被分成2个类,效果较理想,如下图所示
4.4.2. sizes5.mat文件的DBSCAN算法聚类效果
当设置Eps=1.32, MinPts=10时,数据分类数Cluster=4,效果较理想,如下图所示
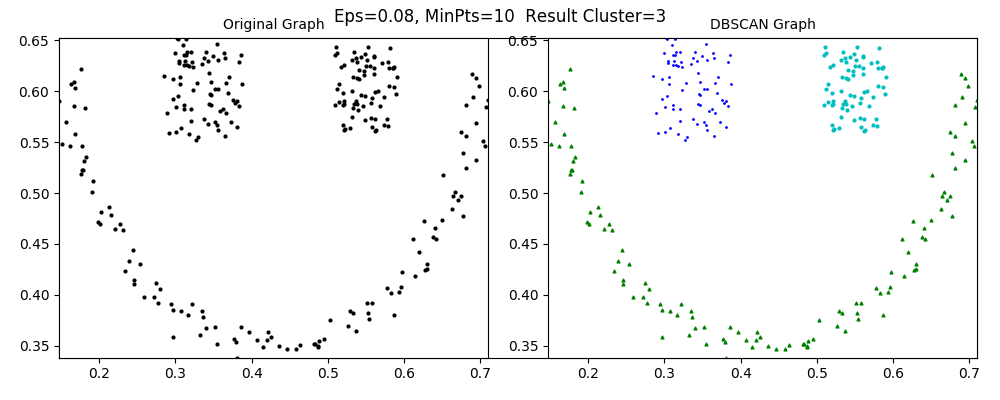
4.4.3. smile.mat文件的DBSCAN算法聚类效果
当设置Eps=0.08, MinPts=10时,数据分类数Cluster=3,效果较理想,如下图所示
4.4.4. spiral.mat文件的DBSCAN算法聚类效果
当设置Eps=1, MinPts=8时,数据分类数Cluster=2,效果较理想,如下图所示
备注
运行平台:Arch Linux
运行环境:Intellij IDEA
待聚类数据集文件:long.mat、moon.mat、sizes5.mat、smile.mat、spiral.mat
源代码:DensityBasedClustering.py