![]()
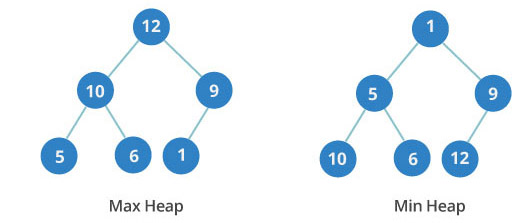
- 堆是一种经过排序的完全二叉树,对其中任一非终端节点,其数据值不大于(或不小于)其左右子节点的值。
- 最小堆(最大堆)堆能保证堆顶元素最小(最大),相比于用数组存放数据,如果要查找所有数据中最小(最大)的数据时,数组的时间复杂度为O(n),而最小堆(最大堆)的时间复杂度为O(1)。
- 而数据增删数据时,需要保证最小堆(最大堆)的动态可维护性仅需O(logN)。因此在特定的需求环境,最小堆(最大堆)这种数据结构非常高效。
1. 最小堆
1.1. 最小堆概念
最小堆,是一种经过排序的完全二叉树,其中任一非终端节点的数据值均不大于其左子节点和右子节点的值。堆内的所有数据中最小的元素始终在堆顶,而增删一个元素而动态维护最小堆性质的时间复杂度仅为O(logN)
1.2. 最小堆实现思路
将最小堆二叉树存储到数组内,非根节点元素的父节点下标为(i-1)/2,若子节点存在则下标为2*i+1。
- 插入操作:每当插入一个元素,将元素插入到容器(数组)尾部,然后执行迭代的上升操作,将插入的元素与其父节点比较,若比父节点小则交换,然后再与交换后节点的父节点相互比较交换,直到放置到合适位置。(最坏递归到根节点终止迭代)
- 取出操作:弹出最小值(即数组首地址元素a[0])。先交换交换堆顶与堆末,再弹出堆末(最小值),然后再将现堆顶元素执行迭代的下降操作,若其子节点存在与其子节点比较,若比子节点小则交换,然后再与交换后的子节点相互比较交换,直到放置在合适位置。(最坏递归到叶子节点)
1.3. 最小堆C++实现完整代码
1.3.1. 最小堆.h文件
文件名:MinHeap.h1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| #ifndef MINHEAP_H_
#define MINHEAP_H_
#include <iostream>
#include <vector>
using namespace std;
#define ElementType int
class MinHeap
{
private:
vector<ElementType> a;
public:
MinHeap(ElementType elements[], int number)
{
for (int i=0; i<number; i++)
{
a.push_back(elements[i]);
}
for (int i=a.size()/2-1; i>=0; i--)
{
down(i);
}
}
void swap(int i, int j)
{
ElementType temp = a[i];
a[i] = a[j];
a[j] = temp;
}
void up(int i)
{
int fa =(i-1)/2;
if (i>0 && a[i]<a[fa])
{
swap(i, fa);
up(fa);
}
}
void push(ElementType p)
{
a.push_back(p);
up(a.size()-1);
}
void down(int i)
{
int son = 2*i+1;
if (son < a.size())
{
if (son+1 < a.size() && a[son] > a[son+1])
{
son++;
}
if (a[i] > a[son])
{
swap(i, son);
}
down(son);
}
}
ElementType pop()
{
ElementType result = a[0];
swap(0, a.size()-1);
a.pop_back();
down(0);
return result;
}
void show()
{
for (int i = 0; i < a.size(); i++)
{
cout << " " << a[i];
}
cout << endl;
}
};
#endif
|
1.3.2. 最小堆.cpp范例代码
文件名:MinHeap.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| #include "MinHeap.h"
int main(void)
{
int a[] = {13, 43, 84, 96, 22, 65, 70, 47};
MinHeap* m = new MinHeap(a, 8);
cout << "显示当前最小堆:" << endl;
m->show();
cout << "弹出最小堆顶的元素:" << m->pop() << endl;
cout << "显示当前最小堆:" << endl;
m->show();
cout << "插入一个节点30:" << endl;
m->push(30);
cout << "显示当前最小堆:" << endl;
m->show();
return 0;
}
|
2. 最大堆
2.1. 最大堆概念
最大堆,是一种经过排序的完全二叉树,其中任一非终端节点的数据值均不小于其左子节点和右子节点的值。
2.2. 最大堆实现思路
将最大堆二叉树存储到数组内,非根节点元素的父节点下标为(i-1)/2,若子节点存在则下标为2*i+1。
- 插入操作:每当插入一个元素,将元素插入到容器(数组)尾部,然后执行迭代的上升操作,将插入的元素与其父节点比较,若比父节点大则交换,然后再与交换后节点的父节点相互比较交换,直到放置到合适位置。(最坏递归到根节点终止迭代)
- 取出操作:弹出最大值(即数组首地址元素a[0])。先交换交换堆顶与堆末,再弹出堆末(最大值),然后再将现堆顶元素执行迭代的下降操作,若其子节点存在与其子节点比较,若比子节点小则交换,然后再与交换后的子节点相互比较交换,直到放置在合适位置。(最坏递归到叶子节点)
2.3. 最大堆C++实现完整代码
2.3.1. 最大堆.h代码
文件名:MaxHeap.h1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| #ifndef MAXHEAP_H_
#define MAXHEAP_H_
#include <iostream>
#include <vector>
using namespace std;
#define ElementType int
class MaxHeap
{
private:
vector<ElementType> a;
public:
MaxHeap(ElementType elements[], int number)
{
for (int i=0; i<number; i++)
{
a.push_back(elements[i]);
}
for (int i=a.size()/2-1; i>=0; i--)
{
down(i);
}
}
void swap(int i, int j)
{
ElementType temp = a[i];
a[i] = a[j];
a[j] = temp;
}
void up(int i)
{
int fa = (i-1)/2;
if (i>0 && a[i] > a[fa])
{
swap(i, fa);
up(fa);
}
}
void push(ElementType p)
{
a.push_back(p);
up(a.size()-1);
}
void down(int i)
{
int son = 2 * i + 1;
if (son < a.size())
{
if (son+1 < a.size() && a[son] < a[son+1])
{
son++;
}
if (a[i] < a[son])
{
swap(i, son);
}
down(son);
}
}
ElementType pop()
{
ElementType result = a[0];
swap(0, a.size()-1);
a.pop_back();
down(0);
return result;
}
void show()
{
for (int i = 0; i < a.size(); i++){
cout << " " << a[i];
}
cout << endl;
}
};
#endif
|
2.3.2. 最大堆.cpp范例代码
文件名:MaxHeap.cpp1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| #include "MaxHeap.h"
int main(void)
{
int a[] = {13,43,84,96,22,65,70,47};
MaxHeap* m = new MaxHeap(a, 8);
cout << "显示当前最大堆:" << endl;
m->show();
cout << "弹出最大堆顶的元素:" << m->pop() << endl;
cout << "显示当前最大堆:" << endl;
m->show();
cout << "插入一个节点90:" << endl;
m->push(90);
cout << "显示当前最大堆:" << endl;
m->show();
return 0;
}
|